semana 7

se realiza el quiz de lo visto en clase

Alcanos:

Los alcanos son hidrocarburos, es decir, compuestos que sólo contienen átomos de carbono e hidrógeno. La fórmula general para alcanos alifáticos (de cadena lineal) es C_nH_2n+2,​ y para cicloalcanos es C_nH_2n.​ También reciben el nombre de hidrocarburos saturados, ya que carecen de enlaces dobles o triples y, por tanto, todos sus carbonos presentan hibridación sp³. Además, carecen de grupos funcionales.

Alquenos:

Los alquenos son hidrocarburos insaturados que tienen uno o varios enlaces carbono-carbono en su molécula. Se puede decir que un alqueno es un alcano que ha perdido dos átomos de hidrógeno produciendo como resultado un enlace doble entre dos carbonos. Los alquenos cíclicos reciben el nombre de cicloalquen

 

Alquinos:

Los alquinos son hidrocarburos alifáticos con al menos un triple enlace (dos enlaces π pi y uno Σ sigma) -C≡C- entre dos átomos de carbono. Se trata de compuestos metaestables debido a la alta energía del triple enlace carbono-carbono. Su fórmula general es C_nH_2n-2.

semana 6

Quimica organica

La Química orgánica o Química del carbono es la rama de la química que estudia una clase numerosa de moléculas, conocidos como compuestos orgánicos, que contienen carbono formando enlaces covalentes carbono-carbono, carbono-hidrógeno y otros heteroátomos.

teoría vitalista

la cual suponía que los compuestos orgánicos jamás podían obtenerse de manera artificial, ya que podían originarse únicamente en los organismos vivos. 1675. Lémerg clasifica a los productos químicos naturales, según sea su origen en: MINERALES, VEGETETALES Y ANIMALES.

hibridacion

En química, se conoce como hibridación a la interacción de orbitales atómicos dentro de un átomo para formar nuevos orbitales híbridos. Los orbitales atómicos híbridos son los que se superponen en la formación de los enlaces, dentro de la teoría del enlace de valencia, y justifican la geometría molecular.

El químico Linus Pauling desarrolló por primera vez la teoría de la hibridación con el fin de explicar la estructura de las moléculas como el metano (CH₄) en 1931.¹​ Este concepto fue desarrollado para este tipo de sistemas químicos sencillos, pero el enfoque fue más tarde aplicado más ampliamente, y hoy se considera una heurística eficaz para la racionalización de las estructuras de compuestos orgánicos.

hibridacion sp3

El átomo de carbono tiene seis electrones: dos se ubican en el orbital 1s (1s²), dos en el 2s (2s²) y los restantes dos en el orbital 2p (2p²). Debido a su orientación en el plano tridimensional el subnivel 2p tiene capacidad para ubicar 6 electrones: 2 en el orbital p_x, dos en el orbital p_y y dos electrones en el orbital p_z. Los dos últimos electrones del carbono se ubicarían uno en el 2p_x, el otro en el 2p_y y el orbital 2p_z permanece vacío (2p_x¹ 2p_y¹). El esquema de lo anterior es (cada flecha un electrón):

hibridacion sp2 

Se define como la combinación de un orbital s y dos orbitales p, para formar 3 orbitales híbridos, que se disponen en un plano formando ángulos de 120º.

Los átomos que forman hibridaciones sp² pueden formar compuestos con enlaces dobles. Forman un ángulo de 120º y su molécula es de forma plana. A los enlaces simples se les conoce como enlaces sigma (σ) y los enlaces dobles están compuestos por un enlace sigma y un enlace pi (). Las reglas de ubicación de los electrones en estos casos, como el alqueno etileno obligan a una hibridación distinta llamada sp², en la cual un electrón del orbital 2s se mezcla sólo con dos de los orbitales 2p: surge a partir o al unirse el orbital s con dos orbitales p; por consiguiente, se producen tres nuevos orbitales sp², cada orbital nuevo produce enlaces covalentes

hibridacion sp

Se define como la combinación de un orbital s y un orbital p, para formar 2 orbitales híbridos, con orientación lineal. Este es el tipo de enlace híbrido, con un ángulo de 180º y que se encuentra existente en compuestos con triples enlaces como los alquinos (por ejemplo el acetileno):

Se caracteriza por la presencia de 2 orbitales pi (π). 

El ciclo de el carbono

es el ciclo biogeoquímico por el cual el carbono se intercambia entre la biosfera, pedosfera, geosfera, hidrosfera y la atmósfera de la Tierra.

formas alotropicas de el carbono

diamante:

 es uno de los alótropos del carbono más conocidos, cuya dureza y alta dispersión de la luz lo hacen útil para aplicaciones industriales y joyería. El diamante es el mineral natural más duro conocido, lo que lo convierte en un abrasivo excelente y le permite mantener su pulido y lustre extremadamente bien. No se conocen sustancias naturales que puedan rayar o cortar un diamante excepto un diamante mismo.

grafito:

El grafito (denominado así por Abraham Gottlob Werner en 1789, del griego γράφειν (graphein, "dibujar/escribir", por su uso en lápices) es uno de los alótropos más comunes del carbono. A diferencia del diamante, el grafito es un conductor eléctrico, y puede ser usado, por ejemplo, como material en los electrodos de una lámpara de arco eléctrico. El grafito tiene la distinción de ser la forma más estable de carbono a condiciones estándar. En consecuencia, es usado en termoquímica como el estado estándar para definir el calor de formación de los compuestos de carbono.

 fullereno :

es una molécula compuesta por carbono que puede adoptar una forma geométrica que recuerda a una esfera, un elipsoide, un tubo (llamado nanotubo) o un anillo. Los fullerenos son la tercera formamolecular estable conocida de carbono, tras el grafito y el diamante.

Semana 5

laboratorio #1

Materiales:

• jeringas

• mecheros

• venoclisis

• bombas

•  palos de pincho

•  bicarbonatos

• vinagre

•  Agua

•  Tuvo de ensayo  
  
  

  • ¿Para qué  nos sirven las leyes de los gases?
   Para conocer su número de moles, presión, volumen, temperatura, presión parcial,
  volumen parcial de un gas y poder ver su capacidad para realizar trabajo en un ciclo
  termodinámico. 

  
  

  Experimento con jeringas

  
  

  tenemos dos jeringas conectadas por medio de un tubo de venoclisis cada una de estas jeringas son de 20 cent y las utilizamos en tres ocasiones 

  
  

  1. verificamos que las dos jeringas tuvieran las mismas cantidades de aire,las dos estaban en la mitad,esto se hace para que el  experimento funcione correctamente .

  2.cuando apretamos una de las dos jeringas (ej 1cm) la otra se baja la misma cantidad (1cm) esto lo hace la presion del gas. 

  3.Cuando se baja una jeringa del todo la otra llega a su tope y Por ultimo utilizamos una sola jeringa con esta colocamos nuestro dedo en su parte inferior esta al no llenarse esta vacía y no sube a su tope

  
  

   

  
  

  Mechero con etanol (C2H6O) y bomba  

     

  Tenemos una bomba a la cual se le hecho solo agua en su interior luego la amarramos, se enciende un mechero el cual tenía en su interior etanol. Colocamos la bomba llena de agua encima de el mechero y esta no se explotó las curiosidad es que nuestra bomba si estallo puede que la bomba tuviera una falla o algo parecido. La energía que se le comunica se invierte en aumentar la temperatura del agua, pero al tener una gran capacidad calorífica necesita mucha energía para aumentar su temperatura.
  
  El calor transferido por la llama se transmite por conduccion a traves de la membrana del globo.

          

  
  

  • Materiales 
  • mechero,globo y agua
  • tubo de ensayo y mechero 
  • prendemos de nuevo el mechero en un tubo de ensayo,colocamos una bomba en parte superior del tubo de ensayo,colocamos un tubo de ensayo encima del mechero y podemos observar que la bomba se infla

  
  

  
  

  Conclusión:

  Al aumentar la temperatura de un gas su volumen aumenta y por esto la boba se onflo. En este experimento se pudo ver la ley de charles.

  
  

  
  

  

  
  

  
  

  Bomba inflada por reacción

  
  

   Se inserta el bicarbonato en la bomba y el vinagre en el tubo, de ensayo, se coloca la bomba sobre el tubo de ensayo y se deja caer el bicarbonato en el vinagre esto forma una reacción química creando un gas que hace que la bomba se infle.

  
  

  
  

  
            

semana 4

 Ley de Graham

formulada en 1829 por el químico británico Thomas Graham, establece que las velocidades de difusión y efusión de los gases son inversamente proporcionales a las raíces cuadradas de sus respectivas masas molares.

Siendo  las velocidades y  las masas molares.

Efusión es el flujo de partículas de gas a través de orificios estrechos o poros.

Se hace uso de este principio en el método de efusión de separación de isótopos.

El fenómeno de efusión está relacionado con la energía cinética de las moléculas. Gracias a su movimiento constante, las partículas de una sustancia se distribuyen uniformemente en el espacio libre. Si hay una concentración mayor de partículas en un punto habrá más choques entre sí, por lo que hará que se muevan hacia las regiones de menor número: las sustancias se efunden de una región de mayor concentración a una región de menor concentración.

ley de gay lussac

​ establece que la presión de un volumen fijo de un gas, es directamente proporcional a su temperatura.

• Si el volumen de una cierta cantidad de gas a presión moderada se mantiene constante, el cociente entre presión y temperatura (kelvin) permanece constante:

o también:

donde:

P es la presión

T es la temperatura absoluta (es decir, medida en kelvin)

k₃ una constante de proporcionalidad

semana 3

Ley de Avogadro

Esta ley relaciona la cantidad de gas (n, en moles) con su volumen en litros (L), considerando que la presión y la temperatura permanecen constantes (no varían).

El enunciado de la ley dice que:

El volumen de un gas es directamente proporcional a la cantidad del mismo.

Esto significa que:

Si aumentamos la cantidad de gas, aumentará el volumen del mismo.

Si disminuimos la cantidad de gas, disminuirá el volumen del mismo.

Esto tan simple, podemos expresarlo en términos matemáticos con la siguiente fórmula:

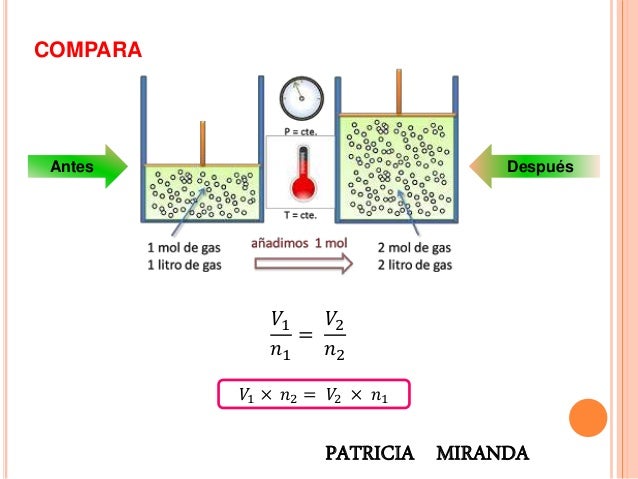
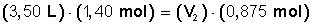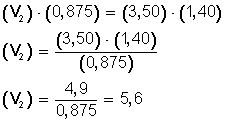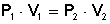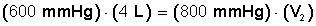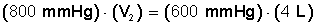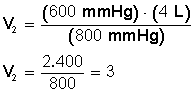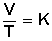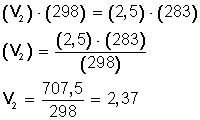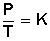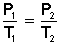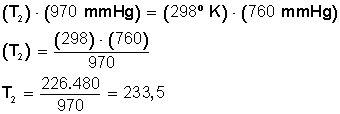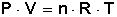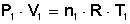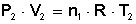que se traduce en que si dividimos el volumen de un gas por el número de moles que lo conforman obtendremos un valor constante.

  

Esto se expresa en la ecuaciónEsto debido a que si ponemos más moles (cantidad de moléculas) de un gas en un recipiente tendremos, obviamente, más gas (más volumen), así de simple.

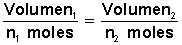 , simplificada es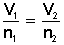 

Veamos un ejemplo práctico y sencillo:

Tenemos 3,50 L de un gas que, sabemos, corresponde a  0,875 mol. Inyectamos gas al recipiente hasta llegar a 1,40 mol, ¿cuál será el nuevo volumen del gas? (la temperatura y la presión las mantenemos constantes).

Solución:

Aplicamos la ecuación de la ley de Avogadro:

y reemplazamos los valores correspondientes:

resolvemos la ecuación, multiplicando en forma cruzada:

Ahora, despejamos V 2 , para ello, pasamos completo a la izquierda el miembro con la incógnita (V 2 ), y hacemos:

Respuesta:

El nuevo volumen (V 2 ), ya que aumentamos los moles hasta 1,40 (n 2 ), es ahora 5,6 L

Ley de Boyle

Esta ley nos permite relacionar la presión y el volumen de un gas cuando la temperatura es constante. 

La ley de Boyle (conocida también como de Boyle y Mariotte) establece que la presión de un gas en un recipiente cerrado es inversamente proporcional al volumen del recipiente, cuando latemperatura es constante .

Lo cual significa que:

El volumen de un gas es inversamente proporcional a la presión que se le aplica:

En otras palabras:

Si la presión aumenta, el volumen disminuye.

Si la presión disminuye, el volumen aumenta.

Esto nos conduce a que, si la cantidad de gas y la temperatura permanecen constantes, el producto de la presión por el volumen siempre tiene el mismo valor .

 

 

Para aclarar este concepto:

Tenemos un cierto volumen de gas (V 1 ) que se encuentra a una presión P 1 . Si variamos la presión a P 2 , el volumen de gas variará hasta un nuevo valor V 2 , y se cumplirá:

que es otra manera de expresar la ley de Boyle.

Apliquemos la fórmula en un ejemplo práctico:

Tenemos 4 L de un gas que están a 600 mmHg de presión. ¿Cuál será su volumen si aumentamos la presión hasta 800 mmHg? La temperatura es constante, no varía.

Solución:

Como los datos de presión están ambos en milímetros de mercurio (mmHg) no es necesario hacer la conversión a atmósferas (atm). Si solo uno de ellos estuviera en mmHg y el otro en atm, habría que dejar los dos en atm.

Aclarado esto, sustituimos los valores en la ecuación P 1 V 1 =  P 2 V 2 .

Ponemos a la izquierda el miembro con la incógnita

Despejamos V 2 :

Respuesta:

Si aumentamos la presión hasta 800 mmHg el volumen disminuye hasta llegar a los 3 L. 

Ley de Charles

Mediante esta ley relacionamos la temperatura y el volumen de un gas cuando mantenemos la presión constante. 

Esta la ley afirma que:

El volumen de un gas es directamente proporcional a la temperatura del gas.

En otras palabras:

Si aumenta la temperatura aplicada al gas, el volumen del gas aumenta.

Si disminuye la temperatura aplicada al gas, el volumen del gas disminuye.

 

Matemáticamente esto se expresa en la fórmulaComo lo descubrió Charles, si la cantidad de gas y la presión permanecen constantes, el cociente entre el volumen (V) y la temperatura (T) siempre tiene el mismo valor (K) (es constante).

lo cual significa que el cociente entre el volumen y la temperatura es constante.

Intentemos ejemplificar:

tenemos un cierto volumen de gas V 1 que se encuentra a una temperatura T 1 . Si aumentamos la temperatura a T 2 el volumen del gas aumentará hasta V 2 , y se cumplirá que:

Esta es  otra manera de expresar la ley de Charles.

•  ejemplo práctico y sencillo:

Un gas  cuya temperatura llega a 25° C tiene un volumen de 2,5 L. Para experimentar, bajamos la temperatura a 10° C ¿Cuál será su nuevo volumen?

Solución:

El primer paso es recordar que en todas estas fórmulas referidas a la temperatura hay que usar siempre la escala Kelvin.

Por lo tanto, lo primero es expresar la temperatura en grados Kelvin:

T 1 = (25 + 273) K= 298 K

T 2 = (10 + 273 ) K= 283 K

Ahora, sustituimos los datos en la ecuación:

Ahora, despejamos V 2 :

Respuesta:

Si bajamos la temperatura hasta los 10º C (283º K) el nuevo volumen del gas será 2,37 L.

Ley de Gay-Lussac

 

Esta ley establece la relación entre la presión (P) y la temperatura (T) de un gas cuando el volumen (V) se mantiene constante, y dice textualmente:

La presión del gas es directamente proporcional a su temperatura.

Esto significa que:

Si aumentamos la temperatura, aumentará la presión.

Si disminuimos la temperatura, disminuirá la presión.
                       

Si lo llevamos al plano matemático, esto queda demostrado con la siguiente ecuación:

la cual nos indica que el cociente entre la presión y la temperatura siempre tiene el mismo valor; es decir, es constante.

Llevemos esto a la práctica y supongamos que tenemos un gas, cuyo volumen (V) no varía, a una presión P 1 y a una temperatura T 1 . Para experimentar, variamos la temperatura hasta un nuevo valor T 2 , entonces la presión cambiará a P 2 , y tendrá que cumplirse la siguiente ecuación:

Esta es la misma Ley de Gay-Lussac expresada de otra forma.

Debemos recordar, además, que esta ley, al igual que la de Charles, está expresada en función de la temperatura absoluta, y tal como en la Ley de Charles, las temperaturas han de expresarse en grados Kelvin.

Veamos un ejemplo:

Tenemos un cierto volumen de un gas bajo una presión de 970 mmHg cuando su temperatura es de 25° C. ¿A qué temperatura deberá estar para que su presión sea 760 mmHg?

Solución:

Lo primero que debemos hacer es convertir los 25º C a grados Kelvin:

T 1 = (25 + 273) K= 298 K

Ahora sustituimos los datos en la ecuación:

Ahora despejamos T 2 :

Respuesta:

La temperatura debe bajar hasta los 233,5º Kelvin. Si convertimos estos grados en grados Celsius hacemos

233,5 − 273 = −39,5 °C.

Ley general de los gases o ecuación general de los gases

Las leyes parciales analizada precedentemente pueden combinarse y obtener una ley o ecuación que relaciones todas las variables al mismo tiempo.

Según esta ecuación o ley general

Esto significa que, si tenemos una cantidad fija de gas y sobre la misma variamos las condiciones de presión (P), volumen (V) o temperatura (T) el resultado de aplicar esta fórmula con diferentes valores, será una constante.

Veamos un ejemplo, para aclarar:

Supongamos que tenemos una cierta cantidad fija de un gas (n 1 ), que está a una presión (P 1 ), ocupando un volumen (V 1 ) a una temperatura (T 1 ).

Estas variables se relacionan entre sí cumpliendo con la siguiente ecuación:

Donde R es una constante universal conocida ya que se puede determinar en forma experimental.

La misma fómula nos permite calcular el volumen molar de un gas (n) :

A modo de experimento, a la misma cantidad fija de gas (n 1 ) le cambiamos el valor a  alguna de las variables tendremos entonces una nueva presión (P 2 ), un nuevo volumen (V 2 ) y una nueva temperatura (T 2 ).

Como ya conocemos le ecuación general colocamos en ella los valores de cada variable:

Según la condición inicial:

Según la condición final:

Vemos que en ambas condiciones la cantidad de gas (n 1 ) es la misma y que la constante R tampoco varía.

Entonces, despejamos n 1 R en ambas ecuaciones:

Entonces, despejamos n 1 R en ambas ecuaciones:

Marcamos con rojo n 1 R para señalar que ambos resultados deben ser iguales entre sí, por lo tanto: